Execução de exemplo com base no problema da Partição. Selecione o projeto TProcuraConstrutiva, e execute. Pode acompanhar o teste excutando as ações localmente.

Sumário

Teste TProcurasConstrutivas
Problema:
  1 - Aspirador
  2 - Puzzle 8
  3 - 8 Damas
  4 - Partição
  5 - Artificial
Opção: 4

Partição - separe os números em duas partes iguais

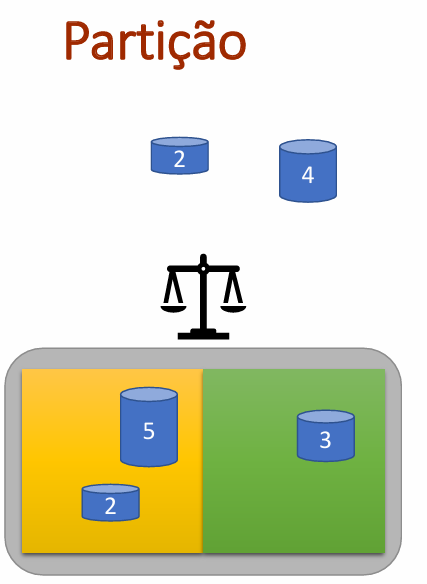
Vamos escolher o problema da partição. Introduza: 4.

Partição
 P1(Algoritmo): Largura Primeiro | P2(Debug): nada | P3(Seed): 1 | P4(Tempo): 10 | P5(Iterações): 0
 P6(Ver): 4 | P7(Limite): 0 | P8(Repetidos): ignorar | P9(pesoAStar): 100 | P10(ruido): 0
 P11(baralhar): 0
Colocar #8: 0 = 0
---   2   2   9   9  ---
---  13  16  17  24  ---
____________________________________________________________________
| 1 - Inicializar | 2 - Explorar | 3 - Parâmetros    | 4 - Solução |
| 5 - Indicadores | 6 - Executar | 7 - Configurações | 8 - Teste   |
Opção:

Este problema consiste em dividir os números em duas partes que somem exatamente o mesmo valor.

Ação 1 - Ver instâncias

Vamos ver as instâncias que temos. Introduza: 1; 10.

ID atual: 10 Intervalo: [2-1000] Prefixo atual: 'instancia_'

Novo ID (ENTER mantém) ou novo prefixo (texto): 10

Existem instâncias de 2 a 1000, correspondendo o ID à quantidade de números. As instâncias são geradas aleatoriamente, podendo existir instâncias impossíveis.

Deixemos a instância 10 para resolução manual.

Ação 2 - Resolver manualmente

Vamos procurar resolver manualmente a intância. Introduza: 2; esq dir esq dir; dir; esq.

g:0 1|2|3
Colocar #8: 0 = 0
---   2   2   9   9  ---
---  13  16  17  24  ---
Ações: esq dir
Sucessor [1-2, ação(ões), exe]:esq dir esq dir
Executadas 4 ações com sucesso.
g:0 6|12|6
Colocar #4: 40 = 30
---   2   2   9   9  ---
     24  16          <<<
>>>  17  13
Ações: esq dir
Sucessor [1-2, ação(ões), exe]:dir
Executadas 1 ações com sucesso.
g:0 8|16|9
Colocar #3: 40 = 39
---   2   2   9      ---
     24  16          <<<
>>>  17  13   9
Ações: esq dir
Sucessor [1-2, ação(ões), exe]:esq
Executadas 1 ações com sucesso.
g:0 10|18|10
Colocar #2: 49 = 39
---   2   2          ---
     24  16   9      <<<
>>>  17  13   9
Ações:
Sem sucessores.
Partição
 P1(Algoritmo): Largura Primeiro | P2(Debug): nada | P3(Seed): 1 | P4(Tempo): 10 | P5(Iterações): 0
 P6(Ver): 4 | P7(Limite): 0 | P8(Repetidos): ignorar | P9(pesoAStar): 100 | P10(ruido): 0
 P11(baralhar): 0
Colocar #2: 49 = 39
---   2   2          ---
     24  16   9      <<<
>>>  17  13   9
____________________________________________________________________

Foi uma boa tentativa, mas no final um lado soma 49 do outro 39, e os números que restam não chegam para equilibrar.

Tal como as 8 damas, o número de ações de uma solução completa é fixo. É igual à quantidade de número a colocar. Sabemos que não faz sentido a procura em largura nestes problemas. Também pelos mesmos motivos que nas 8 damas, não se consegue uma heurística pelo que não faz sentido as procuras informadas.

Naturalmente que se poderia efetuar mais cortes dos que estão a ser feitos nesta implementação. Vamos apenas comparar a remoção de repetidos gerados, relativamente a ignorar repetidos.

No caso da partição, após um número estar num lado, apenas a soma interessa. Como se coloca os números por ordem, um estado fica igual a todos os que têm o montante igual das peças colocadas. Esquerda e direita é naturalmente irrelevante.

Como o estado codificado fica pequeno, a expectativa para ganho por repetidos aumenta.

Ação 3 - Testes Empíricos

Vamos fazer testes empíricos na linha de comandos.

Vamos obter primeiramente a lista de todos os parâmetros.

C:\...\TProcura\Construtiva\Teste> ../../x64/Release/TProcuraConstrutiva -h
PS C:\...\TProcura\Construtiva\Teste> ../../x64/Release/TProcuraConstrutiva -h
 
Teste TProcurasConstrutivas
Problema:
  1 - Aspirador
  2 - Puzzle 8
  3 - 8 Damas
  4 - Partição
  5 - Artificial
Opção: 4
Uso: C:\...\TProcura\x64\Release\TProcuraConstrutiva.exe <instâncias> [opções]
  <instâncias>    Conjunto de IDs: A | A,B,C | A:B[:C]
Opções:
  -R <ficheiro>   Nome do CSV de resultados (omissão: resultados.csv)
  -F <prefixo>    Prefixo dos ficheiros de instância (omissão: instancia_)
  -I <ind>        Lista de indicadores (e.g. 2,1,3)
  -S              Mostrar soluções durante a execução
  -h              Esta ajuda
  -P <expr>       Parâmetros (e.g. P1=1:3 x P2=0:2) - último campo
Exemplo: C:\...\TProcura\x64\Release\TProcuraConstrutiva.exe 1:5 -R out -F fich_ -I 3,1,4,2 -P P1=1:5 x P6=1,2
   Executar sem argumentos entra em modo interativo, para explorar todos os parametros e indicadores
 
Lista de parâmetros:
 P1(Algoritmo): Largura Primeiro (1 a 7)
 P2(Debug): nada (0 a 4)
 P3(Seed): 1 (1 a 1000000)
 P4(Tempo): 10 (1 a 3600)
 P5(Iterações): 0 (0 a 1000000000)
 P6(Ver): 4 (1 a 100)
 P7(Limite): 0 (-1 a 1000000)
 P8(Repetidos): ignorar (1 a 3)
 P9(pesoAStar): 100 (0 a 10000)
 P10(ruido): 0 (-100 a 100)
 P11(baralhar): 0 (0 a 1)
 
Lista de indicadores:
 
I1(Custo): 1º lugar (o resultado é o custo da solução atual)
I2(Tempo(ms)): 2º lugar (Tempo em milisegundos da execução (medida de esforço computacional).)
I3(Iterações): 3º lugar (Iterações do algoritmo, intrepretadas conforme o algoritmo (medida de esforço independente do hardware).)
I4(Expansões): 4º lugar (número de expansões efetuadas)
I5(Gerações): 5º lugar (número de estados gerados)
I6(Lower Bound): 6º lugar (valor mínimo para a melhor solução, se igual ao custo da solução obtida, então esta é ótima)

Temos para teste a procura em profundidade ilimitada, e pretendemos comparar ignorar estados repetidos, ou remover todos os repetidos gerados.

PS ...\Teste> TProcuraConstrutiva 10:19 -R resultadoParticao -P P7=-1 P1=3 x P8=1,3
...
Opção: 4
...
Ficheiro resultadoParticao.csv gravado.

Podemos ver o resultado:

Rótulos de Linha	Soma de I1(Custo) 1:ignorar	3:gerados	Soma de I2(Tempo(ms)) 1:ignorar	3:gerados	Soma de I4(Expansões) 1:ignorar	3:gerados
10	8	8	0	15	27	27
11	10	10	0	4	17	17
12	-1	-1	1	5	947	119
13	-1	-1	0	4	1151	143
14	14	14	0	4	24	24
15	15	15	0	5	25	25
16	-1	-1	6	5	17403	440
17	-1	-1	8	4	24223	462
18	-1	-1	17	5	46639	630
19	-1	-1	21	6	57931	580
Total Geral	41	41	53	57	148387	2467

As instâncias escolhidas são muito pequenas, e o tempo de execução é praticamente nulo. Não servem para medir diferenças de tempo, mas servem para medir diferenças no número de estados expandidos. Tudo leva a crer que a remoção de repetidos gerados é muito vantajosa.

Vamos procurar instâncias maiores, de 20 a 29.

PS ...\Teste> TProcuraConstrutiva 20:29 -R resultadoParticaoB -P P7=-1 P1=3 x P8=1,3
...
Opção: 4
...
Ficheiro resultadoParticaoB.csv gravado.

Rótulos de Linha	Soma de I1(Custo) 1:ignorar	3:gerados	Soma de I2(Tempo(ms)) 1:ignorar	3:gerados	Soma de I4(Expansões) 1:ignorar	3:gerados
20	18	18	0	14	87	85
21	21	21	0	4	46	46
22	21	21	0	4	35	35
23	-1	-1	134	7	390983	1236
24	-1	-1	381	5	1071431	1164
25	25	25	0	4	41	41
26	25	25	0	4	66	65
27	-1	-1	2420	5	8098059	2104
28	-1	-1	2431	8	7867847	2186
29	29	29	0	4	49	49
Total Geral	135	135	5366	59	17428644	7011

É agora claro que a remoção de repetidos gerados é crítica para o desempenho. Podemos ver também que as instâncias que não têm solução, são muito mais difíceis. Nestas instâncias toda a árvore de estados é percorrida, e podemos registar diferenças entre ter ou não remoção de repetidos, de várias ordens de grandeza.

Qual é a maior instância que se conseguimos resolver com esta implemantação?

Resposta:

Vamos usar apenas a remoção de repetidos. Como não sabemos qual é a maior instância que se consegue resolver, e o melhor método tem um tempo insignificante na maior instância testada, a 29, fazemos primeiramente um teste de 10 em 10, até 200, para termos uma ideia.

PS ...\Teste> TProcuraConstrutiva 30:200:10 -R resultadoParticaoC -P P7=-1 P1=3 P8=3
...
Opção: 4
...
Ficheiro resultadoParticaoC.csv gravado.

Rótulos de Linha	Soma de I1(Custo)	Soma de I2(Tempo(ms))	Soma de I4(Expansões)
30	30	15	50
40	-1	10	7301
50	50	4	83
60	60	3	142
70	70	6	119
80	79	4	132
90	-1	79	74065
100	-1	132	130625
110	108	4	314
120	-1	230	222208
130	-1	291	269323
140	140	4	236
150	149	5	252
160	-1	710	604753
170	-1	814	655988
180	178	4	376
190	190	5	673
200	198	4	339
Total Geral	1245	2324	1966979

Todas as instâncias a baixo de 1 segundo, mas mesmo assim já perto do limite dos 10 segundos. A instância 100 levou 0.1 segundos, a 160 levou 0.7 segundos, pelo que o limite estará algures entre 200 e 300. Assim, vamos testar a partir de 200, até 300, passos de 5.

Rótulos de Linha	Soma de I1(Custo)	Soma de I2(Tempo(ms))	Soma de I4(Expansões)
205	-1	1638	1251882
210	-1	1399	1107437
215	-1	1824	1407324
220	-1	1906	1516272
225	224	4	382
230	230	4	392
235	234	4	398
240	239	5	463
245	245	5	417
250	250	5	425
255	254	5	433
260	259	5	439
265	265	5	450
270	270	5	460
275	-2	10001	6974880
280	280	5	1041
285	-2	10001	7132853
290	-2	10001	7017596
295	-2	10001	6435970
300	299	5	511
Total Geral	3037	46828	32850025

A instância 275 não se consegue resolver em 10 segundos, mas a 220 sim. As instâncias com solução, são mais simples, pelo que perturbam a análise. A instância impossível maior que se consegue resoolver, estará entre 220 e 275.

Naturalmente que com outra semente aleatória, iriamos ter instâncias diferentes, que podem ser mais complexas ou mais simples.