Execução de exemplo com base no problema do Aspirador. Pode acompanhar o teste executando as ações localmente.
Sumário
- Ação 10 - Procura em Profundidade
- Ação 11 - Efetuar uma procura em Profundidade Primeiro
- Ação 12 - Ver uma árvore de procura maior
- Ação 13 - Profundidade Iterativa
- Ação 14 - Profundidade ilimitada
- Ação 15 - Desafio Procura Profundidade
┌─ Teste TProcuraConstrutiva ──┐
│ 1 - Aspirador │
│ 2 - Puzzle 8 │
│ 3 - 8 Damas │
│ 4 - Partição │
└──────────────────────────────┘
Opção: 1
Selecione o problema do Aspirador: 1.
Ação 10 - Procura em Profundidade
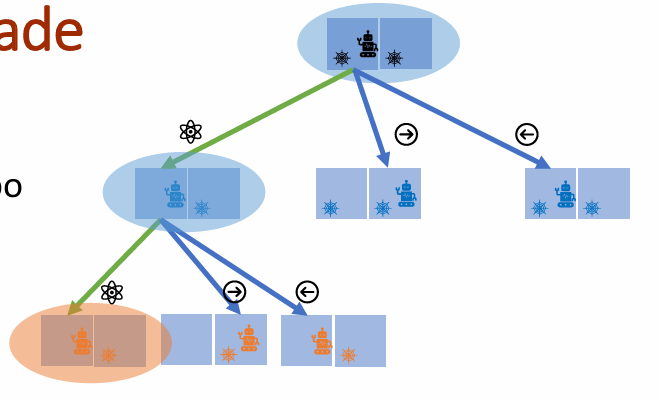
Avançamos agora para a procura em profundidade. Neste caso temos neste algoritmo diversas estratégias. Podemos executar esta procura com um limite de profundidade. Vamos fazer isso na instância 2, que sabemos ter uma solução de 3 movimentos.
Ação 11 - Efetuar uma procura em Profundidade Primeiro
Utilizar a instância número 2, o algoritmo profundidade primeiro, com limite de profundidade a 3, com nível de debug máximo, ignorando repetidos e ver ações a 1: 1; 2; 3; 1; 3; 7; 3; 2; 4; 8; 1; 6; 1; ENTER; 6.
O parâmetro 1 é o algoritmo, em que o 3 é a profundidade primeiro.
┌─ ⚙ P1(ALGORITMO) ─────────────────────────────────────────────────── │ Algoritmo base a executar. │ 1: Largura Primeiro │ 2: Custo Uniforme │ 3: Profundidade Primeiro │ 4: Melhor Primeiro │ 5: A* │ 6: IDA* │ 7: Branch and Bound └────────────────────────────────────────────────────────────────────── ALGORITMO (atual 1): 3
O parâmetro 7 é o limite, com diferentes interpretações conforme o algoritmo.
Na procura em largura o limite servia para limitar o número de estados gerados mas não expandidos. Aqui serve para limitar o nível de profundidade, que é fixado a 3.
Opção: 6 ═╤═ ► Execução iniciada ═══ ├■═╤═ 💰 g:0 ═══ │ * [*] │ ├■═╤═ 🔖 1 💰 g:1 ⚖ 1|2 ═══ ⚡ esq │ │ [*] * │ │ ├■═╤═ 🔖 3 💰 g:2 ⚖ 2|4 ═══ ⚡ dir │ │ │ * [*] │ │ │ 🍃 🪜 │ │ └■═╤═ 🔖 4 💰 g:2 ⚖ 2|4 ═══ ⚡ asp │ │ [.] * │ │ 🍃 🪜 │ └■═╤═ 🔖 2 💰 g:1 ⚖ 2|4 ═══ ⚡ asp │ * [.] │ ├■═╤═ 🔖 5 💰 g:2 ⚖ 3|6 ═══ ⚡ esq │ │ [*] . │ │ 🍃 🪜 │ └■═╤═ 🔖 6 💰 g:2 ⚖ 3|6 ═══ ⚡ asp │ * [.] │ 🍃 🪜 ├─ Parâmetros ─ P1=3 P2=4 P3=1 P4=10 P5=0 P6=1 P7=3 P8=1 P11=0 ═╧═ 🏁 Execução terminada ⏱ ═══ Aspirador ┌─ ⚙ Parâmetros ────────────────────────────────────────────────────── │ P1(ALGORITMO): Profundidade Primeiro | P2(NIVEL_DEBUG): COMPLETO | P3(SEMENTE): 1 │ P4(LIMITE_TEMPO): 10 | P5(LIMITE_ITERACOES): 0 | P6(VER_ACOES): 1 | P7(LIMITE): 3 │ P8(ESTADOS_REPETIDOS): ignorar | P11(BARALHAR_SUCESSORES): 0 └────────────────────────────────────────────────────────────────────── * [*] ┌─ ⚖ Indicadores ───────────────────────────────────────────────────── │ I1(IND_CUSTO): -1 | I2(Tempo(ms)): 0 | I3(Iterações): 0 | I4(IND_EXPANSOES): 3 | │ I5(IND_GERACOES): 6 | I6(IND_LOWER_BOUND): 0 └────────────────────────────────────────────────────────────────────── ┌─ ☰ Menu ─────────┬────────────────┬─────────────────────┬──────────────┐ │ 1 📄 Instância │ 2 🔍 Explorar │ 3 ⚙ Parâmetros │ 4 ✔ Solução │ │ 5 ⚖ Indicadores │ 6 ► Executar │ 7 🛠️ Configurações │ 8 🧪 Teste │ └───────────────────┴────────────────┴─────────────────────┴──────────────┘ Opção:
Podemos ver todos os estados gerados. A árvore tendo 3 níveis, permite dois movimentos, pelo que não foi descoberta a solução, retornando -1. No último nível há um nó folha, indicando que é final da árvore, e motivo, neste caso uma escada a simbolizar o limite da procura.
Embora o indicador 6 não seja atualizado, este resultado pode ser utilizado para saber que não há nenhuma solução de comprimento inferior a 3, ou seja, é um lower bound, neste caso 3, já que o custo de cada movimento é unitário.
Esta visualização da árvore da procura é interessante para pequenos problemas, mas naturalmente que procuras maiores torna-se impraticável. Podemos observar aqui que o estado inicial foi gerado novamente, com etiqueta 3, dado que estamos a ignorar os repetidos.
Ação 12 - Ver uma árvore de procura maior
Colocar a profundidade a 10, e o nível de debug a 3, ver ações a 4: 1; 2; 3; 7; 10; 2; 3; 6; 4; ENTER; 6.
Opção: 6 ═╤═ ► Execução iniciada ═══ ├■═╤═ 💰 g:0 ═══ │ ├■═╤═ 🔖 1 💰 g:1 ⚖ 1|2 ═══ ⚡ esq │ │ ├■═╤═ 🔖 3 💰 g:2 ⚖ 2|4 ═══ ⚡ dir │ │ │ ├■═╤═ 🔖 5 💰 g:3 ⚖ 3|6 ═══ ⚡ esq │ │ │ │ ├■═╤═ 🔖 7 💰 g:4 ⚖ 4|8 ═══ ⚡ dir │ │ │ │ │ ├■═╤═ 🔖 9 💰 g:5 ⚖ 5|10 ═══ ⚡ esq │ │ │ │ │ │ ├■═╤═ 🔖 11 💰 g:6 ⚖ 6|12 ═══ ⚡ dir │ │ │ │ │ │ │ ├■═╤═ 🔖 13 💰 g:7 ⚖ 7|14 ═══ ⚡ esq │ │ │ │ │ │ │ │ ├■═╤═ 🔖 15 💰 g:8 ⚖ 8|16 ═══ ⚡ dir │ │ │ │ │ │ │ │ │ ├■═╤═ 🔖 17 💰 g:9 ⚖ 9|18 ═══ ⚡ esq │ │ │ │ │ │ │ │ │ │ [*] * ─── 🍃 🪜 │ │ │ │ │ │ │ │ │ └■═╤═ 🔖 18 💰 g:9 ⚖ 9|18 ═══ ⚡ asp │ │ │ │ │ │ │ │ │ * [.] ─── 🍃 🪜 │ │ │ │ │ │ │ │ └■═╤═ 🔖 16 💰 g:8 ⚖ 9|18 ═══ ⚡ asp │ │ │ │ │ │ │ │ ├■═╤═ 🔖 19 💰 g:9 ⚖ 10|20 ═══ ⚡ dir │ │ │ │ │ │ │ │ │ . [*] ─── 🍃 🪜 │ │ │ │ │ │ │ │ └■═╤═ 🔖 20 💰 g:9 ⚖ 10|20 ═══ ⚡ asp │ │ │ │ │ │ │ │ [.] * ─── 🍃 🪜 │ │ │ │ │ │ │ └■═╤═ 🔖 14 💰 g:7 ⚖ 10|20 ═══ ⚡ asp │ │ │ │ │ │ │ ├■═╤═ 🔖 21 💰 g:8 ⚖ 11|22 ═══ ⚡ esq │ │ │ │ │ │ │ │ ├■═╤═ 🔖 23 💰 g:9 ⚖ 12|24 ═══ ⚡ dir │ │ │ │ │ │ │ │ │ * [.] ─── 🍃 🪜 │ │ │ │ │ │ │ │ └■═╤═ 🔖 24 💰 g:9 ⚖ 12|24 ═══ ⚡ asp │ │ │ │ │ │ │ │ [.] . │ │ │ │ │ │ │ │ 🎯 Solução encontrada! 💰 g:9 │ │ │ │ │ │ │ │ │ [.] . ─── 🎯 9 → 📈 ─── { 🔖 22 } ─── { 🔖 12 } ─── { 🔖 10 } ─── { 🔖 8 } ─── { 🔖 6 } ─── { 🔖 4 } ─── { 🔖 2 } ├─ Parâmetros ─ P1=3 P2=3 P3=1 P4=10 P5=0 P6=4 P7=10 P8=1 P11=0 ═╧═ 🏁 Execução terminada ⏱ ═══ Aspirador ┌─ ⚙ Parâmetros ────────────────────────────────────────────────────── │ P1(ALGORITMO): Profundidade Primeiro | P2(NIVEL_DEBUG): DETALHE | P3(SEMENTE): 1 │ P4(LIMITE_TEMPO): 10 | P5(LIMITE_ITERACOES): 0 | P6(VER_ACOES): 4 | P7(LIMITE): 10 │ P8(ESTADOS_REPETIDOS): ignorar | P11(BARALHAR_SUCESSORES): 0 └────────────────────────────────────────────────────────────────────── [.] . ┌─ ⚖ Indicadores ───────────────────────────────────────────────────── │ I1(IND_CUSTO): 9 | I2(Tempo(ms)): 0 | I3(Iterações): 0 | I4(IND_EXPANSOES): 12 | │ I5(IND_GERACOES): 24 | I6(IND_LOWER_BOUND): 0 └────────────────────────────────────────────────────────────────────── ... Opção:
Com o nível debug a 3 vemos a árvore de procura sem os estados expandidos, mas vemos as ações. Vemos no entanto todos os estados folha, o que pode ser importante para conhecer os estados cortados. A informação é mais reduzida, e poderá ser uma boa forma de analisar e ver a árvore, o que com a informação completa dos estados poderia já não ser possível.
Vemos que no nível 10 os estados são todos nós folha, o que permite que o algoritmo evolua em largura, alcançando um estado solução.
Notar que ao retornar, os estados gerados não expandidos são mostrados no final de cada ramo. Assim, é possível confirmar a totalidade de estados gerados e quando foram expandidos.
A solução não é óptima, tem comprimento 9! Podemos visualizar a solução, introduza: 4.
Opção: 4
══ ✔ Solução ══
* [*] (💰 g:0) ⚡ → esq → dir → esq → dir
* [*] (💰 g:4) ⚡ → esq → dir → asp → esq
[*] . (💰 g:8) ⚡ → asp
[.] . (💰 g:9) 🎯
Como o algoritmo é cego, segue a ordem dos sucessores. Neste caso está sempre a trocar de posição antes de aspirar. Notar que houve a primeira parte da solução que andou da esquerda para a direita, ficando igual ao estado inicial.
Apenas foi ver as alternativas quando teve de voltar para trás, devido ao limite de profundidade. Se tivéssemos escolhido uma profundidade menor, a solução obtida seria também menor. Mas se a profundidade fosse menor que a solução mais curta, não iriamos obter nenhuma solução.
É com base nesse dilema que surge a procura em profundidade iterativa, no caso deste código é executada com o limite=0.
Ação 13 - Profundidade Iterativa
Colocar a profundidade iterativa (limite a 0), e o nível de debug a 2: 1; 2; 3; 7; 0; 2; 2; ENTER; 6.
Opção: 6 ═╤═ ► Execução iniciada ═══ ├─────────── 🌳 🪜 1 ⏱ ──────────── ├■═╤═ 💰 g:0 ═══ ─── 🍃 🪜 ├─────────── 🌳 🪜 2 ⏱ ──────────── ├■═╤═ 💰 g:0 ═══ │ ├■═╤═ 🔖 1 💰 g:1 ⚖ 1|2 ═══ ⚡ esq ─── 🍃 🪜 │ └■═╤═ 🔖 2 💰 g:1 ⚖ 1|2 ═══ ⚡ asp ─── 🍃 🪜 ├─────────── 🌳 🪜 3 ⏱ ──────────── ├■═╤═ 💰 g:0 ⚖ 1|2 ═══ │ ├■═╤═ 🔖 3 💰 g:1 ⚖ 2|4 ═══ ⚡ esq │ │ ├■═╤═ 🔖 5 💰 g:2 ⚖ 3|6 ═══ ⚡ dir ─── 🍃 🪜 │ │ └■═╤═ 🔖 6 💰 g:2 ⚖ 3|6 ═══ ⚡ asp ─── 🍃 🪜 │ └■═╤═ 🔖 4 💰 g:1 ⚖ 3|6 ═══ ⚡ asp │ ├■═╤═ 🔖 7 💰 g:2 ⚖ 4|8 ═══ ⚡ esq ─── 🍃 🪜 │ └■═╤═ 🔖 8 💰 g:2 ⚖ 4|8 ═══ ⚡ asp ─── 🍃 🪜 ├─────────── 🌳 🪜 4 ⏱ ──────────── ├■═╤═ 💰 g:0 ⚖ 4|8 ═══ │ ├■═╤═ 🔖 9 💰 g:1 ⚖ 5|10 ═══ ⚡ esq │ │ ├■═╤═ 🔖 11 💰 g:2 ⚖ 6|12 ═══ ⚡ dir │ │ │ ├■═╤═ 🔖 13 💰 g:3 ⚖ 7|14 ═══ ⚡ esq ─── 🍃 🪜 │ │ │ └■═╤═ 🔖 14 💰 g:3 ⚖ 7|14 ═══ ⚡ asp ─── 🍃 🪜 │ │ └■═╤═ 🔖 12 💰 g:2 ⚖ 7|14 ═══ ⚡ asp │ │ ├■═╤═ 🔖 15 💰 g:3 ⚖ 8|16 ═══ ⚡ dir ─── 🍃 🪜 │ │ └■═╤═ 🔖 16 💰 g:3 ⚖ 8|16 ═══ ⚡ asp ─── 🍃 🪜 │ └■═╤═ 🔖 10 💰 g:1 ⚖ 8|16 ═══ ⚡ asp │ ├■═╤═ 🔖 17 💰 g:2 ⚖ 9|18 ═══ ⚡ esq │ │ ├■═╤═ 🔖 19 💰 g:3 ⚖ 10|20 ═══ ⚡ dir ─── 🍃 🪜 │ │ └■═╤═ 🔖 20 💰 g:3 ⚖ 10|20 ═══ ⚡ asp │ │ 🎯 Solução encontrada! 💰 g:3 │ │ │ [.] . ─── 🎯 3 → 📈 ─── { 🔖 18 } ├─ Parâmetros ─ P1=3 P2=2 P3=1 P4=10 P5=0 P6=4 P7=0 P8=1 P11=0 ═╧═ 🏁 Execução terminada ⏱ ═══ Aspirador ┌─ ⚙ Parâmetros ────────────────────────────────────────────────────── │ P1(ALGORITMO): Profundidade Primeiro | P2(NIVEL_DEBUG): PASSOS | P3(SEMENTE): 1 │ P4(LIMITE_TEMPO): 10 | P5(LIMITE_ITERACOES): 0 | P6(VER_ACOES): 4 | P7(LIMITE): 0 │ P8(ESTADOS_REPETIDOS): ignorar | P11(BARALHAR_SUCESSORES): 0 └────────────────────────────────────────────────────────────────────── [.] . ┌─ ⚖ Indicadores ───────────────────────────────────────────────────── │ I1(IND_CUSTO): 3 | I2(Tempo(ms)): 0 | I3(Iterações): 0 | I4(IND_EXPANSOES): 10 | │ I5(IND_GERACOES): 20 | I6(IND_LOWER_BOUND): 0 └────────────────────────────────────────────────────────────────────── ... Opção:
Podemos observar que o algoritmo encontrou a solução de comprimento 3, a solução ótima. Fez várias iterações que não serviram para nada, antes de executar na iteração 4 com limite a 4. Cada iteração fica marcada com a sinalética de árvore, e com a escada com o limite da árvore. Essas árvores de procura a mais, são muito mais pequenas que a árvore final, pelo que o peso de executar essas procuras extra não é muito relevante.
As iterações que não serviram para nada, é na verdade uma afirmação pouco precisa. Serviram para saber que não há solução nesse nível. Apenas assim é que se pode concluir na iteração 4 que a solução é óptima. Executando a procura em profundidade com limite 4, obtínhamos a solução ótima, mas sem saber que é ótima.
Podemos ver também a versão compactada da árvore de procura, contendo apenas informação do estado, tal como na procura em largura, mas desta vez com informação de onde o estado veio. Há uma só linha por cada estado expandido. Os estados gerados não expandidos são em muito menor número, e estão em ramos ainda não explorados, sendo indicados no final, tal como nos outros níveis de debug. Pela observação da árvore é possível verificar que a maior parte das ramificações são de dois sucessores, o que é natural dado que este problema tem apenas duas salas.
Vamos agora ver o que acontece se não limitarmos a procura em profundidade, colocando o limite=-1
Ação 14 - Profundidade ilimitada
Colocar a profundidade ilimitada (limite a -1), e o nível de debug a 1: 1; 2; 3; 7; -1; 2; 1; ENTER; 6.
Opção: 6
Segmentation fault (core dumped)
Temos um crash do programa, e bem cedo. Como a procura em profundidade está implementada de forma recursiva, houve um problema no stack. Se tivesse implementada com listas, teríamos um problema de memória, como na procura em largura. Entrou-se num ramo infinito, mesmo neste pequeno problema, como aliás é possível imaginar após conhecermos a solução da procura com nível 10.
Ação 15 - Desafio Procura Profundidade
Lembra-se de algo dado na procura em largura, que impede ciclos infinitos e poderia permitir o uso da procura em profundidade ilimitada?
Resposta
Sim, não ignorar os estados repetidos não servem apenas para reduzir a árvore de procura. Evitam também ciclos infinitos. Com repetidos nos ascendentes ou gerados, consegue resolver com a procura em profundidade ilimitada, qualquer uma das 50 instâncias.
Está terminado esta execução de exemplo. Este problema tem uma heurística perfeita, pelo que, qualquer algoritmo informado encontra a solução ótima sem nunca se enganar. Iremos em outros problemas testar os algoritmos informados.
O custo de cada ação é sempre unitário, pelo que, o custo uniforme será mostrado num problema em que cada ação possa ter custo variável. As configurações e os testes empíricos, com as opções 7 e 8 do menu, são exemplificadas em outros problemas.
