| TesteTVector | Aspirador 1 | Aspirador 2 | Puzzle 8 | 8 Damas | Partição | Artificial | 8 Damas CI | 8 Damas CP | Partição CB |
Execução de exemplo com base no problema do Aspirador. Selecione o projeto TProcuraConstrutiva, e execute. Pode acompanhar o teste excutando as ações localmente.
Sumário
- Ação 1 - Trocar de instância
- Ação 2 - Explorar os sucessores
- Ação 3 - Ver a solução/caminho realizada manualmente
- Ação 4 - Ver a alterar um parâmetro
- Ação 5 - Efetuer uma procura em Largura
- Ação 6 - Editar opções A
- Ação 7 - Editar opções B
- Ação 8 - Resolver outra instância
- Ação 9 - Desafio Procura em Largura
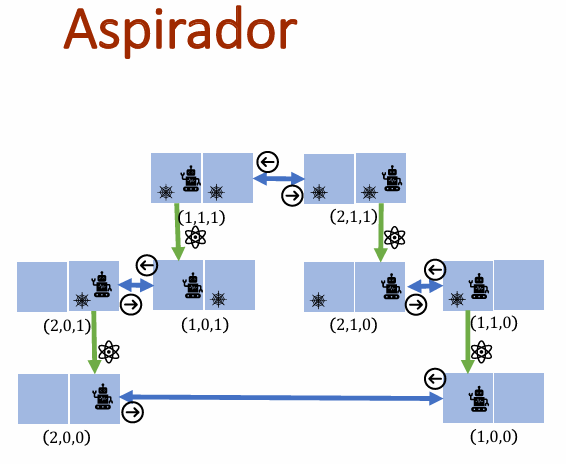
Selecione o problema do Aspirador: 1.
A versão deste problema foi generalizada no código para poderem existir N salas, uma ou lado das outras, e não apenas 2 como no manual, sendo em tudo o resto igual.
Esta é a informação apresentada no teste manual. Na zona superior aparece o nome do problema, seguido dos parametros e valores atuais. Podemos ver que o primeiro parametro é o algoritmo, e está selecionado de omissão a Largura Primeiro. Em termos de Debug está selecionado o valor nada, ou seja, não é mostrada informação de debug. Seguem-se outros parametros, os quais alguns serão apresentados ao longo desta execução.
Temos também o estado atual, que tem uma visualização dependente do problema.
Após o estado temos o menu, com as opções de inicializar numa nova instância, explorar o espaço de estados, editar os parâmetros atuais, ver a solução atual, escolher os indicadors a calcular após execução, executar o algoritmo selecionado com os parametros atuais, editar configurações e executar um teste empírico com as configurações atuais.
Tanto os parâmetros como o menu, repetem-se em cada interação. Para evitar repetição na documentação, o output é cortado sempre que não existam ambiguidades.
Ação 1 - Trocar de instância
Escreva os seguintes números separados por Enter: 1; 2
Temos hipótese aqui de alterar o prefixo da instância, útil para situações em que se lê os dados da instância de um ficheiro. Este problema as instâncias são geradas aleatoriamente, e não lidas de ficheiros, pelo que escolhemos apenas o ID da instância.
Tínhamos inicialmente uma instância com 4 salas, estando o aspirador na terceira sala, estando as duas primeiras sujas:
Agora temos uma instância com 2 salas, estando ambas sujas, e o aspirador está na segunda: A representação do estado é algo que é implementado na sub-classe (neste caso em CAspirador::Debug()), de modo a se poder visualizar o estado em que estamos. Ao chamar Inicializar() podemos trocar o ID da instância. Para este problema o ID é utilizado para definir a dimensão da instância, e assim podemos escolher em ter uma instância maior ou menor. A sujidade das casas é gerada aleatoriamente. No entanto a semente aleatória é um parâmetro (P3(Seed): 1), sendo sempre a mesma caso não se altere, garantindo assim que podemos obter a mesma instância mais tarde.
Ação 2 - Explorar os sucessores
A partir do estado atual, introduza: 2; 1; 2.
Podemos ver que o estado atual tem dois sucessores, o aspirador pode ir para a sala da esquerda, ou aspirar a sala atual. Escolhemos o primeiro estado, e depois escolhemos o segundo, aspirar. Os sucessores são visualizados pelas suas ações, existindo três possíveis ações: esq, dir, asp. Para indicar o número do sucessor, é preciso ver, já que o número 1 é para a primeira ação válida, na lista de sucessores. No entanto, as ações são unívocas. Podemos indicar várias ações de uma só vez.
Neste momento estamos na sala da esquerda, com a sala limpa, mas a sala da direita está suja. Complete os movimentos necessários para limpar ambas as salas, e saia da exploração dos sucessores. Utilize desta vez o nome das ações e não número, introduzido duas ações de uma vez. Introduza: dir asp; ENTER. Note que "dir asp" podem ser introduzidas de uma vez.
Ao receber as duas ações, estas foram executadas e indicado o número de ações executados com sucesso. Se fosse uma solução completa, todas as ações até ao estado final, esta operação seria uma verificação da solução. Caso exista alguma ação inválida, a ação é rejeitada e o estado atual fica na primeira ação inválida. Assim, é possível verificar ou identificar erros em soluções obtidas por métodos externos, sendo apresentada a evidência de falha.
Para um problema novo, é sempre importante que explore os sucessores, nomeadamente procure resolver instâncias pequenas no modo manual. Tem duas vantagens: identifica bugs que tenha na sua implementação; ganha entendimento sobre o problema em questão, que lhe poderá levar a identificar optimizações que de outra forma lhe passariam desapercebidas.
Ação 3 - Ver a solução realizada manualmente
O resultado da resolução manual da ação anterior, é visualizar apenas o último estado. No entanto houve um caminho, que ficou guardado. Introduza: 4.
Neste problema uma solução é um conjunto de ações, o caminho desde o estado inicial até ao estado final. É mostrado esse caminho visualizando as ações a partir do estado inicial. Foram 4 movimentos, mas houve um desperdício. No primeiro movimento, poderíamos ter logo aspirado. Em outros problemas, a solução pode ser apenas o estado final. Notar ainda na letra g, seguida de um número. Esta letra representa o custo g(n) no manual, e sempre que ocorra significa o custo desde o estado inicial até esse estado. Neste problema o custo não foi definido, pelo que é adoptado o valor de 1 unidade por cada movimento.
A visualizaçãop de ações é mais curta e simples, mas podemos ver todos os estados também. Para isso é preciso alterar o parâmetro P6(Ver).
Ação 4 - Ver a alterar um parâmetro
Vamos editar o parâmetro P6(Ver). Introduza: 3
Podemos ver todos os os parâmetros e valores mínimos e máximos.
Podemos também editar qualquer parâmetro, como é o caso, o parâmetro 6, tem o valor 4, e pretendemos colocar a 1. Caso seja definido no problema novos parâmetros, ficariam aqui também expostos ao utilizador para edição. Introduza: 6; 1; ENTER; 4.
Vemos agora a solução, o caminho com todos os estados intermédios do estado inicial até ao estado final.
Ação 5 - Efetuer uma procura em Largura
Coloque na instância inicial, número 2, com nível de debug máximo: 1; 2; 3; 2; 4; ENTER; 6.
A opção 1 já sabemos, inicia uma instância, neste caso 2. A opção 4 vamos alterar neste caso o parâmetro nível de debug. Há vários níveis de debug, sendo o 4 o valor que mostra a informação mais completa, embora extensa.
A opção 6 executa o algoritmo selecionado, que é a Largura Primeiro.
Verificar que o número de expansões é 6 e gerações é 12. O resultado da procura é 3, sendo recolhido pelo I1(custo). Significa que a procura encontrou uma solução de comprimento 3. Notar que o I3(Iterações) e I6(Lower Bound) ficaram a 0, já que não são atualizados neste algoritmo.
No caso de não ter os resultados iguais, confirme se todos os parâmetros estão iguais.
Podemos ver a solução, tendo ficado guardada, tal como na resolução manual. Introduza: 4.
Verifique que tem apenas 3 movimentos, ao contrário dos 4 obtidos na resolução manual.
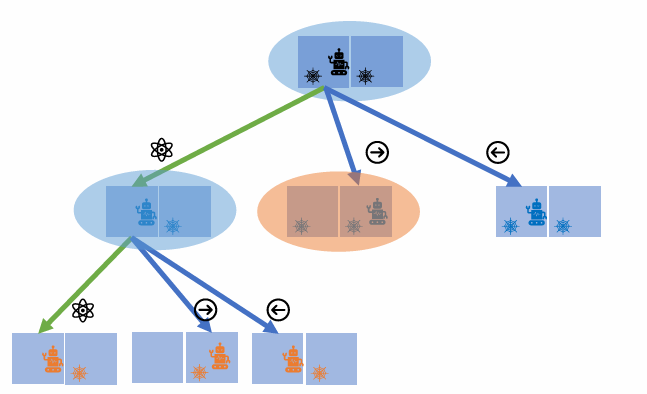
A árvore da procura em largura não é desenhada na visualização textual, apenas na procura em profundidade. Nesta procura o que podemos ver é cada estado expandido e respetivos sucessores gerados. Cada estado irá aparecer pela primeira vez quando é gerado, e uma segunda vez quando é expandido. Na procura em largura, expandimos sempre o estado gerado há mais tempo.
- Verificar que o segundo estado expandido, é o primeiro sucessor do primeiro estado expandido. O terceiro estado expandido é o segundo sucessor do primeiro estado expandido. Poder-se-ia continuar, o estado expandido seguinte é sempre o gerado há mais tempo.
Temos no entanto o mesmo estado inicial a ser gerado. De facto, o primeiro sucessor na segunda expansão, é o primeiro estado que é gerado novamente.
Podemos lidar com estados repetidos de duas formas:
- Verificar se o estado a ser gerado, não tem já um ascendente - neste caso é preciso implementar a função Distinto() - Para fazer esta validação, o código tem de seguir pelos pais, e testar se são diferentes do atual.
- Verificar se o estado a ser gerado, não foi já gerado mesmo em outro ramo, desde que no mesmo nível ou anterior. Nesse caso o estado pode ser excluído, já que já terá sido tratado nesse outro ramo - para ter esta opção, é preciso implementar a função Codificar() que coloca o estado num vetor de bits - o código utiliza uma hashtable com perdas, para verificar se o estado já foi criado em tempo constante, não existindo problemas de memória mesmo em execuções longas devido às perdas.
Ação 6 - Editar opções A
Altere a opção para remover os repetidos com base nos ascendentes, e o debug para nível 3: 1; 2; 3; 8; 2; 2; 3; ENTER; 6.
- Verificar que o número de expansões é 5 e gerações é 6, uma melhoria. O resultado da procura mantém-se em 3.
A interação de troca de parâmetro não é mais mostrada para não saturar o texto.
Podemos ver o nível de debug a 3. Tem apenas os estados expandidos, mas não vemos os estados gerados. Mesmo assim podemos confirmar que o estado inicial não foi gerado, caso contrário seria expandido na 4º ou 5º expansão.
Ação 7 - Editar opções B
Alterar a opção para remover os repetidos com base nos gerados, e alterar o debug para nível 2: 1; 2; 3; 8; 3; 2; 2; ENTER; 6.
Podemos ver que o estado já não é mostrado. Em cada expansão é mostrado o custo (g), seguido de dois números: expansões e gerações realizadas até ao momento. No caso deste problema o estado é visualizado numa só linha, mas em outros problemas estes dois níveis de debug podem fazer diferença. Notar que não houve alteração no número de expansões e gerações, muito embora a técnica para lidar com os estados repetidos seja distinta.
É importante observar a procura em instâncias pequenas, para poder observar ineficiências, como os estados repetidos, ou mesmo bugs.
O nível de debug 1 insere um # por cada 1000 expansões, de modo a dar alguma noção de como vai a procura, e o nível 0 não dá qualquer informação.
Ação 8 - Resolver outra instância
Repor a opção de ignorar os repetidos, colocar o debug no nível 1, e procurar resolver uma instância maior: 1; 10; 3; 8; 1; 2; 1; ENTER; 6.
Pode haver um problema de memória. A instância é demasiado grande, e sem remover repetidos, rapidamente gera demasiados estados:
São demasiados estados gerados, 1,5 milhões, em 0.5 segundos. Há um # que é colocado no output a cada 1000 expansões. Se desconfiamos que com tanto estado, dificilmente a solução pode ser óptima, podemos ver a solução. Introduza: 4
Não houve desperdício visivel nesta solução. O algoritmo procura em largura garante-nos que esta solução é ótima, dado que o custo de cada ação é unitário.
Para lidar com o problema de memória, podíamos limitar a procura em largura com o parâmetro limite, fixando a 100 ou 1000 estados, mas perdendo a optimalidade.
A melhor solução para lidar com este problema é eliminar estados repetidos, idealmente todos os gerados. Mas se mesmo assim a procura em largura resultar num problema de memória, a utilização de um limite, poderá ser uma opção, mantendo-se apenas um determinado número limitado de estados gerados não expandidos. Esta abordagem perde a optimalidade, e também a garantia de construir um caminho do estado inicial ao final, o que poderá não ser problemático em alguns problemas.
Ação 9 - Desafio Procura em Largura
Com a procura em largura, até que tamanho consegue obter a solução ótima do aspirador?
Resposta:
Depende das condições de execução, vamos colocar na resposta o VPL com a 512MB. Consegue resolver com P8(Repetidos)=gerados, até à instância 19, existindo problema de memória na instância 20. Num computador pessoal pode variar, e o limite de tempo pode ocorrer antes do problema de memória. Limitando a 1000 e mantendo os replicados gerados, a procura em largura consegue resolver até à instancia 50, a maior considerada no código. A utilização do limite não permite garantir a otimalidade da solução A utilização de repetidos com base nos ascendentes, permite também resolver o problema de memória, mas ganha-se o problema de tempo, sendo uma solução viável até à instância 44, mantendo o tempo limite em 10 segundos.
| TesteTVector | Aspirador 1 | Aspirador 2 | Puzzle 8 | 8 Damas | Partição | Artificial | 8 Damas CI | 8 Damas CP | Partição CB |