| TesteTVector | Aspirador 1 | Aspirador 2 | Puzzle 8 | 8 Damas | Partição | Artificial | 8 Damas CI | 8 Damas CP | Partição CB |
Execução de exemplo com base no problema das 8 Damas. Selecione o projeto TProcuraConstrutiva, e execute. Pode acompanhar o teste excutando as ações localmente.
Sumário
- Ação 1 - Ver instâncias
- Ação 2 - Resolver manualmente
- Ação 3 - Procura em Largura
- Ação 4 - Procura em Profundidade
- Ação 5 - Heurística
- Ação 6 - Testes Empíricos
Vamos entrar no problema das 8 damas. Introduza: 3.
Este estado vazio é um tabuleiro de 8x8. O objetivo é colocar damas no tabuleiro de xadrez, sem que as damas se ataquem mutuamente.
Ação 1 - Ver instâncias
Vamos ver que instâncias temos. Introduza: 1; 4.
O tabuleiro foi generalizado a largura N. Podemos escolher entre 4 e 40 colunas.
Ação 2 - Resolver manualmente
Há várias formas de se colocar damas no tabuleiro. Está implementada a colocação de uma dama, na linha superior que não esteja atacada.
Poder-se-ia permitir a colocação de uma dama em qualquer posição. No entanto, como em cada linha tem de estar uma dama, optamos por colocar sempre na primeira linha vazia. Caso se tivessem implementado diferentes opções, seria adicionado um parametro, e os sucessores seria distinto conforme o valor desse parâmetro.
Vamos resolver esta instância manualmente, para explorar o espaço de estados. Introduza: 2; d1; d4; d2.
Esta resolução correu mal, e chegamos a um beco sem saida. Não há nenhuma coluna onde possa ser colocada a quarta dama, sem que esteja atacada.
A escolha na primeira ação por d2 (ou d3), é crítica para obter a solução.
Neste problema a solução em sempre o mesmo número de ações, igual a N.
Ação 3 - Procura em Largura
Vamos fazer uma procura em largura, no tabuleiro de 4x4, debug completo. Vamos deixar desde já fixado o limite no número de iterações a 1000000. Introduza: 1; 4; 3; 2; 4; 5; 1000000; ENTER; 6.
A solução foi encontrada. No entanto, o algoritmo explora todos os estados do nível 3 antes de ver o primeiro do nível 4. Neste problema, como a solução está no nível 4, acaba por não ser muito interessante esta procura. Não só este algoritmo gasta muito tempo nos níveis inferiores, a explorar completamente, como a procura em profundidade ilimitada não tem problema, já que não existem ciclos infinitos.
Ação 4 - Procura em Profundidade
Vamos executar a mesma instância com a procura em profundidade ilimitada. Introduza: 1; 4; 3; 1; 3; 7; -1; ENTER; 6.
Podemos observar que o algoritmo em profundidade fez o mesmo erro que nós fizemos, ao escolher d1. No entanto, após ver que não é possível, testa a opção de d2 e encontra a solução.
Neste caso fez 8 expansões, contra 13 da procura em largura. Mas evidentemente que não será esta pequena instância que irá suportar as nossas conclusões. Temos um teste empírico na ação 6, com mais instâncias.
Ação 5 - Heurística
Na abordagem construtiva, atendendo a que este problema tem o número de ações fixas, se as ações tivessem custo variável, faria sentido uma heurística para estimar o custo. Sendo o custo fixo, apenas sabemos que se existir solução, a distância é conhecida e igual para todos os estados num determinado nível. Assim, não faz sentido construir uma heurítsica, nem ter procuras informadas com a abordagem construtiva.
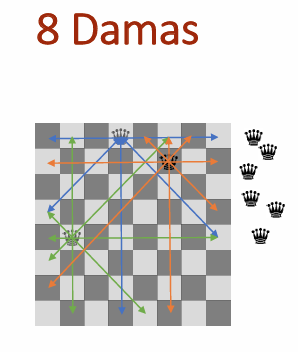
Poder-se-ia ter no entanto opções que melhorariam a abordagem construtiva. Uma das possibilidades é considerar ou não os estados repetidos. Neste problema temos 3 eixos de simetria. Significa que a mesma posição pode ao ser refletida em cada eixo, transformar-se numa das outras, num total de 8 posições simétricas. Ao anular as simetrias por normalização do estado, e remoção de repetidos, o espaço de estados reduz-se. As simetrias estão implementadas, pelo que vamos testar na próxima ação.
Outra possibilidade não implementada neste código, é a verificação se há linhas/colunas vazias, que estejam totalmente atacadas. Ao colocar duas ou três damas, estas podem cobrir a totalidade das casas da última linha, e essa linha só é analisada no último nível. Esta implementação causa também mais peso, mas invalida estados antecipadamente.
Ação 6 - Testes Empíricos
Nos testes empíricos vamos passar para a interface da linha de comando, por ser mais simples.
Vamos obter primeiramente a lista de todos os parâmetros.
Num primeiro teste pretendemos comparar a procura em largura com a procura em profundidade ilimitada, e respetivas versões com eliminação de estados repetidos. Colocamos o P7=-1 para a procura em profundidade ilimitada, não afetando a procura em largura.
Soma de I2(Tempo(ms)):
| Rótulos de Linha | 1:Largura Primeiro 1:ignorar | 3:gerados | 3:Profundidade Primeiro 1:ignorar | 3:gerados |
|---|---|---|---|---|
| 4 | 0 | 15 | 0 | 4 |
| 5 | 0 | 5 | 0 | 4 |
| 6 | 1 | 5 | 0 | 4 |
| 7 | 0 | 5 | 0 | 4 |
| 8 | 1 | 5 | 0 | 4 |
| 9 | 3 | 13 | 0 | 4 |
| 10 | 15 | 56 | 0 | 5 |
| 11 | 80 | 182 | 0 | 4 |
| 12 | 447 | 901 | 0 | 4 |
| 13 | 2417 | 5171 | 0 | 4 |
| Total Geral | 2964 | 6358 | 0 | 41 |
Podemos ver a clara superioridade da procura em profundidade ilimitada. Todas as instâncias são resolvidas, mas em termos de tempo, a última leva 2 e 5 segundos pela procura em largura, e 0 segundos na procura em profundidade.
Soma de I4(Expansões):
| Rótulos de Linha | 1:Largura Primeiro 1:ignorar | 3:gerados | 3:Profundidade Primeiro 1:ignorar | 3:gerados |
|---|---|---|---|---|
| 4 | 13 | 8 | 8 | 8 |
| 5 | 33 | 18 | 5 | 5 |
| 6 | 114 | 60 | 31 | 31 |
| 7 | 419 | 211 | 9 | 9 |
| 8 | 1665 | 839 | 113 | 113 |
| 9 | 6977 | 3490 | 41 | 41 |
| 10 | 30779 | 15392 | 102 | 102 |
| 11 | 149131 | 74567 | 52 | 52 |
| 12 | 773731 | 386869 | 261 | 261 |
| 13 | 4250877 | 2125440 | 111 | 111 |
| Total Geral | 5213739 | 2606894 | 733 | 733 |
Em termos de expansões, o máximo da procura em profundidade é algumas centenas, enquanto que a procur em largura tem na instância maior mais de um milhão de expansões. A remoção de estados gerados repetidos, podemos observar na procura em largura que reduz em metade o número de expansões, mas duplica o tempo.
Não é possível com estas instâncias, observar diferença para a procura em profundidade.
Vamos retirar as duas primeiras configurações do teste, para poder executar instâncias maiores.
| Rótulos de Linha | Soma de I2(Tempo(ms)) 1:ignorar | 3:gerados | Soma de I4(Expansões) 1:ignorar | 3:gerados |
|---|---|---|---|---|
| 14 | 1 | 19 | 1899 | 1899 |
| 15 | 1 | 6 | 1359 | 1359 |
| 16 | 5 | 12 | 10052 | 2850 |
| 17 | 2 | 19 | 5374 | 5206 |
| 18 | 24 | 105 | 41299 | 28605 |
| 19 | 2 | 29 | 2545 | 4656 |
| 20 | 131 | 410 | 199635 | 112596 |
| 21 | 5 | 98 | 8562 | 20208 |
| 22 | 1070 | 1812 | 1737188 | 425154 |
| 23 | 19 | 1137 | 25428 | 250250 |
| Total Geral | 1260 | 3647 | 2033341 | 852783 |
Podemos ver que o tempo continua menor se não se eliminarem os estados repetidos, mesmo na instância mais complexa, a 22, que levou 1 segundo, enquanto que com eliminação de repetidos foi 1,8 segundos. No entanto, para essa instância o número de expansões foi de 1737188 ignorando repetidos, e de 425154 eliminando repetidos. Confirma-se que neste problema, e também para o algoritmo em profundidade, a eliminação de repetidos reduz o número de expansões, mas aumenta o tempo, pelo que não é compensador.
As instâncias pares aparentam ser mais complexas que as ímpares.
Qual é afinal a maior instância que se consegue resolver?
Resposta:
Vamos usar apenas as instâncias pares, e até ao limite de 40, que é o que temos implementado. Utilizamos apenas a procura em profundidade ilimitada, sem eliminação de repetidos.
| Rótulos de Linha | Soma de I1(Custo) | Soma de I2(Tempo(ms)) | Soma de I4(Expansões) |
|---|---|---|---|
| 24 | 24 | 309 | 411608 |
| 26 | 26 | 323 | 397699 |
| 28 | 28 | 2537 | 3006298 |
| 30 | -2 | 10001 | 10677294 |
| 32 | -2 | 10001 | 9980585 |
| 34 | -2 | 10001 | 9346319 |
| 36 | -2 | 10001 | 8628941 |
| 38 | -2 | 10001 | 7673544 |
| 40 | -2 | 10001 | 7353868 |
| Total Geral | 66 | 63175 | 57476156 |
Consegue-se resolver até à instância 28, em 2 segundos. Nas instâncias 30 a 40, não se consegue encontrar solução no limite de 10 segundos.
| TesteTVector | Aspirador 1 | Aspirador 2 | Puzzle 8 | 8 Damas | Partição | Artificial | 8 Damas CI | 8 Damas CP | Partição CB |